 제6차 솔베이회의가 열린 1930년 브뤼셀을 걷고 있는 아인슈타인과 보어. 아인슈타인은 승리를 확신한 듯 여유로운데 비해 보어는 초조한 모습이다. 아인슈타인의 절친인 폴 에렌페스트가 찍었다. 오른쪽 상단은 아인슈타인의 '광 상자' 사고실험의 개요을 보어가 그린 그림.
제6차 솔베이회의가 열린 1930년 브뤼셀을 걷고 있는 아인슈타인과 보어. 아인슈타인은 승리를 확신한 듯 여유로운데 비해 보어는 초조한 모습이다. 아인슈타인의 절친인 폴 에렌페스트가 찍었다. 오른쪽 상단은 아인슈타인의 '광 상자' 사고실험의 개요을 보어가 그린 그림.
1930년 제6차 솔베이회의에서 아인슈타인은 양자역학을 반박하는 두 번째 사고실험을 제시했습니다. 공격 대상은 이번에도 불확정성 원리였습니다. 물론 궁극정인 목적은 양자역학의 불완전성을 밝히기 위한 것이었습니다.
아인슈타인의 공격
아인슈타인은 이번에도 천재성이 번뜩이는 사고실험을 내놓았습니다. 위의 그림 같은 상자를 상상합니다. 상자에는 작은 구멍이 하나 있는데, 셔트를 통해 그 구멍을 열고 닫을 수 있습니다. 그리고 그 셔트를 열고 닫는 시간 간격은 상자 안의 시계에 의해 제어됩니다. 상자는 극히 민감한 용수철로 연결되어 있기 때문에 자(scale)의 눈금을 통해 질량의 변화를 측정할 수 있습니다.
아인슈타인의 논증은 다음과 같습니다.
상자에 빛을 가득 채우고 상자의 무게를 잰다. 광자 한 개가 상자에서 빠져나올 만큼의 짧은 시간 T 동안 셔트를 연 다음 닫는다. 그 다음 다시 상자의 무게를 잰다. 광자 한 개는 특정한 에너지(E = ℎν, 플랑크 상수 ℎ와 진동수 ν의 곱)를 갖는다. 그리고 E = mc² 공식에 따라 광자 한 개의 유효 질량을 구할 수 있다. 따라서 광자 한 개가 상자를 빠져나가면 상자의 무게는 그만큼 가벼워진다.
아인슈타인의 주장은 이렇다. 우리는 상자의 무게를 정확하게 잴 수 있다. 그러므로 상자의 질량, 즉 에너지 불확정성 ΔE는 0이다. 그런데 이런 변화가 생긴 데 걸린 시간의 불확정성 Δt는 T로 유한한 값이다. 그러므로 시간 불확정성과 에너지 불확정성의 곱(ΔE × Δt)은 0이다. 이 같은 결과는 상보적인 물리량인 에너지 변화와 시간 변화의 곱이 플랑크 상수값 이상이 되어야 한다는 불확정성 원리를 만족시키지 않는다. 따라서 불확정성 원리는 문제가 있다.
(위치와 운동량에 대한 불확정성 원리의 수식 ΔxΔp≥ℏ는 수학적 조작을 조금 하면 시간과 에너지에 대한 불확정성 원리의 수식 ΔEΔt≥ℏ로 변환된다.)
아인슈타인은 이 같은 논증을 통해 승리를 확신했습니다. 보어의 공동연구자인 레온 로젠펠트는 그 상황을 다음과 같이 묘사했습니다.
"그것은 보어에게 큰 엄청난 충격이었음에 틀림없습니다. 그는 처음엔 반박논리를 찾을 수 없어 무척 당황하는 모습이었습니다. 그날 저녁 내내 보어는 극도로 불안해보였습니다. 보어는 물리학자들을 이리저리 찾아다니며 “뭔가 잘못된 게 틀림없어요. 만약 아인슈타인이 옳다면 물리학은 끝장이에요.”라며 설득하기도 했습니다. 하지만 그는 반박논리를 찾지 못했습니다.
나는 그들이 클럽을 떠날 때의 두 적대자의 이미지를 결코 잊지 못할 것입니다. 약간 아이러니한 미소를 지으며 조용히 걷는 키가 크고 위풍당당한 모습의 아인슈타인과 흥분에 가득 차서 그의 옆에서 종종걸음으로 따라가는 보어... 하지만 그 다음날 아침 상황은 극적으로 역전되었습니다. 승자는 보어였습니다."
보어의 방어
보어는 밤새 한잠도 자지 못하고 해답 찾기에 골몰했습니다. 마침내 새벽녘 영감이 머리를 스쳤습니다. 그 단초는 다름 아닌 아인슈타인의 일반상대성이론이었습니다. 보어는 상자의 무게를 측정하는 과정을 명쾌하게 생각하는 것으로 시작했습니다.
아인슈타인은 광자가 방출되는 시간과 광자 방출 전후의 상자 무게를 정확하게 잴 수 있다고 하였습니다. 보어는 바로 그 대목의 허점을 정확하게 파고들었습니다. 그는 아인슈타인의 ‘상자 안의 시계’ 사고실험을 그림으로 그리고 아인슈타인의 논증을 다음과 같이 반박했습니다.
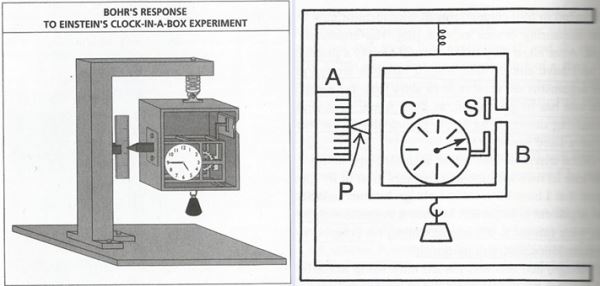 1930년 제6차 솔베이회의에서 아인슈타인이 보어에게 제기한 '광 상자' 사고실험을 분석해 보어가 그린 그림(왼쪽). 오른쪽은 이를 한층 이해하기 쉽게 간략하게 그린 도해.
1930년 제6차 솔베이회의에서 아인슈타인이 보어에게 제기한 '광 상자' 사고실험을 분석해 보어가 그린 그림(왼쪽). 오른쪽은 이를 한층 이해하기 쉽게 간략하게 그린 도해.
우리는 불확정성 원리에 의해 상자의 무게를 지시하는 계기판 바늘의 위치 불확정성 Δq와 이의 상보적인 물리량인 상자의 운동량 불확정성 Δp의 존재를 인정해야 합니다. Δp의 정보를 얻기 위해서는 그 상자의 질량을 측정해야 하는데 그 정확도의 한계, 즉 불확정성 Δm이 존재합니다. 따라서 gTΔm≥Δp(gTΔmΔq≥h)의 관계가 성립합니다(g는 중력상수).
이쯤에서 보어의 결정타가 나옵니다. 아인슈타인의 일반상대성이론에 의하면 중력장은 시간의 흐름 속도를 변화시킵니다. 상자 안의 광자가 방출되고 나면 상자의 무게가 줄게 됩니다. 상자가 중력장 내에 있고 상자의 용수철이 움직이므로(눈금이 변화하므로) 상자 안의 시계바늘 속도도 변합니다. Δq가 시간 간격 불확정성 ΔT를 야기하는 것입니다.
상자의 운동량 불확정성 Δp는 에너지 불확정성 ΔE와 연결되어 있습니다. gTΔm≥Δp에서 ΔEΔT≥ℏ라는 수식을 유도해낼 수 있습니다. 즉 불확정성 원리가 성립합니다. 아인슈타인의 논증은 오류입니다.
(적색편이 공식에 의하면 시간 T의 불확정성 ΔT=gTΔq/c², ΔE = c²Δm. and so ΔEΔT=gTΔqΔm=gTΔmΔq≥ℏ. We have therefore proven the claimed ΔEΔT≥ℏ)
이상과 같은 보어의 논증을 간단히 설명하면 이렇게 됩니다. 아인슈타인은 일정 시간 간격 동안 상자의 에너지 변화를 정확하게 잴 수 있다고 했으나, 보어는 광자가 방출되면(에너지 변화) 중력장의 변화가 발생하고 이로 인해 시간 간격마저 변화하므로 여전히 에너지와 시간이라는 상보적인 물리량 사이에 불확정성 원리가 성립한다고 논증한 것입니다. 상자의 무게를 정확하게 재려면, 즉 계기판의 눈금 Δq의 불확정성을 작게 하려면 광자 한 개가 방출되는 시간 간격 T가 길어져야 한다는 것은 당연해 보입니다.
아인슈타인은 보어의 논증을 수용할 수밖에 없었습니다. 이번에도 보어는 아인슈타인의 공격을 막아냈고, 아인슈타인은 패했습니다. 그렇다고 아인슈타인이 불확정성 원리와 양자론이 완전하다고 인정한 것은 아니었습니다. 그 반대로 더욱 정교한 논증을 개발할 결심을 했을 따름입니다. 아니나 다를까, 이로부터 5년 뒤에 1935년 아인슈타인은 미국에서 그의 동료 포돌스키, 로젠과 함께 양자론을 공격하는 강력한 논증(EPR)을 발표했습니다.
Bohr-Einstein Debates 2 : The Photon Box Thought Experiment – Quantum Odyssey 15
 Einstein and Bohr walking in Brussels in 1930 at the 6th Solvay Conference. Einstein is relaxed as if he was sure of victory, but Bohr is nervous. Photographed by Einstein's close friend, Paul Ehrenfest.
Einstein and Bohr walking in Brussels in 1930 at the 6th Solvay Conference. Einstein is relaxed as if he was sure of victory, but Bohr is nervous. Photographed by Einstein's close friend, Paul Ehrenfest.
At the 6th Solvay Conference in 1930, Einstein presented a second thought experiment that refuted quantum mechanics. The target of attack was again the uncertainty principle. Of course, the ultimate purpose was to reveal the incompleteness of quantum mechanics.
Einstein's argument
Einstein once again came up with a thought experiment that sparked genius.
Einstein's thought experiment of 1930 as designed by Bohr. Einstein's Box(Photon Box) was supposed to prove the violation of the Uncertainty relation between time and energy.
Imagine a box like the picture above. There is one small hole in the box, which can be opened and closed through the shutter. And the time interval between opening and closing that shutter is controlled by a clock inside the box. Since the box is connected by an extremely sensitive spring, the change in mass can be measured by reading the scale.
Einstein's argument is as follows.
Fill the box full of photon and weigh the box. Open the shutter for a short time T, long enough for one photon to escape the box, then close it. Then weigh the box again. One photon has a specific energy (E = ℎν, Planck's constant ℎ times the frequency ν). And the effective mass of one photon can be calculated according to the E = mc² formula. Therefore, when one photon exits the box, the weight of the box is reduced by that much.
Einstein's argument is this. We can accurately weigh the box. Therefore, the box's mass, or energy uncertainty ΔE, is zero. However the uncertainty of the time taken for this change Δt is T, which is finite. Therefore the product of time uncertainty and energy uncertainty (ΔEΔt) is zero. Such a result does not satisfy the uncertainty principle that the product of the energy change and the time change, which are complementary physical quantities, must be greater than the value of Planck's constant. So the uncertainty principle is wrong.
(The expression of the uncertainty principle for position and momentum, ΔxΔp≥ℏ is converted to the expression for the uncertainty principle for time and energy, ΔEΔt≥ℏ, with a little mathematical manipulation.)
Einstein was confident of his victory with this same argument. Bohr's collaborator, Leon Rosenfeld, described the situation as follows:
It was a real shock for Bohr...who, at first, could not think of a solution. For the entire evening he was extremely agitated, and he continued passing from one scientist to another, seeking to persuade them that it could not be the case, that it would have been the end of physics if Einstein were right; but he couldn't come up with any way to resolve the paradox. I will never forget the image of the two antagonists as they left the club: Einstein, with his tall and commanding figure, who walked tranquilly, with a mildly ironic smile, and Bohr who trotted along beside him, full of excitement...The morning after saw the triumph of Bohr.
Bohr's Resonse
Bohr couldn't sleep all night and was engrossed in finding answers. At last dawn inspiration crossed his mind. It was none other than Einstein's general theory of relativity. Bohr began by thinking clearly about the process of weighing a box.
Einstein said that he could accurately measure the time the photon was emitted and the weight of the box before and after the photon was emitted. Bohr precisely dug the loophole of the passage. He drew a picture of Einstein's 'Photon Box' thought experiment and refuted Einstein's argument as follows.
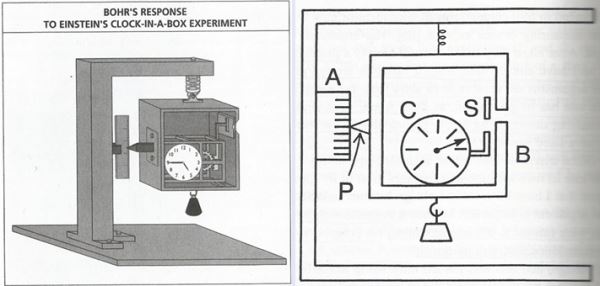 A drawing (left) drawn by Bohr after analyzing the 'Photon Box' thought experiment proposed by Einstein to Bohr at the 6th Solvay Conference in 1930. The diagram on the right is a simplified diagram to make it easier to understand.
A drawing (left) drawn by Bohr after analyzing the 'Photon Box' thought experiment proposed by Einstein to Bohr at the 6th Solvay Conference in 1930. The diagram on the right is a simplified diagram to make it easier to understand.
According to the uncertainty principle, we must admit the existence of the uncertainty of the position of the measurement pointer Δq, which dictates the weight of the box. And the uncertainty of the momentum of the box Δp, which is a physical quantity complementary to this. In order to obtain the information of
Δp, the mass of the box must be measured. but there is a limit to its accuracy, that is, the uncertainty Δm. Therefore, the relationship gTΔm≥Δp (gTΔmΔq≥h) holds (g is the gravitational constant).
This is where Bohr's final blow comes in. According to Einstein's general theory of relativity, gravitational fields change the rate of passage of time. After the photons inside the box are emitted, the weight of the box is reduced. Because the box is in a gravitational field and the spring in the box is moving (since the scale changes), the speed of the clock hands inside the box also changes. Δq causes the time interval uncertainty ΔT.
The momentum uncertainty Δp of the box is linked to the energy uncertainty ΔE. From gTΔm≥Δp, the expression ΔEΔT≥ℏ can be derived. That is, the uncertainty principle holds. Einstein's argument is fallacious.
(By the redshift formula, the uncertainty of time ΔT=gTΔq/c², ΔE=c²Δm. and so ΔEΔT=gTΔqΔm=gTΔmΔq≥ℏ. We have therefore proven the claimed ΔEΔT≥ℏ)
The simple explanation of Bohr's argument as above is as follows. Einstein said that it was possible to accurately measure the change in the energy of the box over a certain time interval. But Bohr argued that when a photon is emitted (energy change), the gravitational field changes and the time interval also changes, so the uncertainty principle still holds between the complementary physical quantities of energy and time. It seems obvious that to accurately weigh the box, i.e., to reduce the uncertainty of the pointer Δq on the measurement panel, the time interval T between each photon emission must be long.
Einstein had no choice but to accept Bohr's argument. Again, Bohr succeeded in defending against Einstein's attack, and Einstein was defeated.
However, Einstein did not admit that the uncertainty principle and quantum theory were complete. On the contrary, he only resolved to develop a more sophisticated argument. Sure enough, five years after this in 1935, Einstein along with his colleagues Podolsky and Rosen published a powerful argument (EPR) against quantum theory in the United States.
<pinepines@injurytime.kr>